Elliptic Curve Signature Algorithm (ECDSA)

Overall Description

Elliptic Curves over Finite Fields

Let p > 3 be an odd prime. An elliptic curve E over Fp is defined by an equation of the form

\[y^2 = x^3 + ax + b\]

where a, b ∈ Fp, and 4a³ + 27b² ≢ 0 (mod p). The set E (Fp) consists of all point (x, y), x ∈ Fp, y ∈ Fp, which satisfy the defining equation, together with a special point O called the point at infinity.

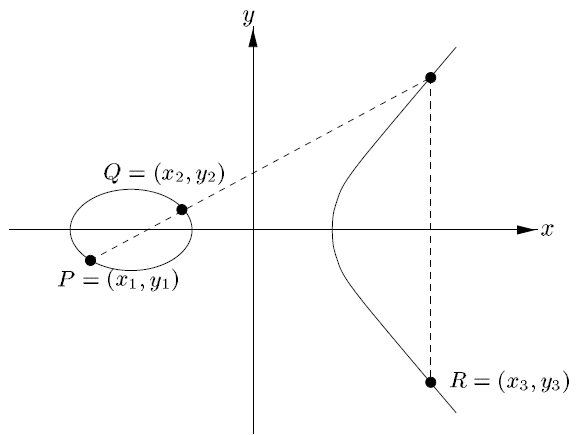
The following algebraic formula for the sum of two points and the double of a point can now be derived from the geometric description.

1. P + O = O + P = P for all P ∈ E(Fp)

2. If P = (x,y) ∈ E(Fp), then (x,y) + (x,-y) = O

3. (Point addition) Let P = (x1,y1) ∈ E(Fp) and Q = (x2,y2) ∈ E(Fp), where P ≠ ±Q. Then P + Q = (x3,y3), where

   \[x3 = \left(\frac{y2-y1}{x2-x1}\right)^2 - x1 - x2 \quad \text{and} \quad y3 = \left(\frac{y2-y1}{x2-x1}\right)^2(x1 - x3) - y1\]

4. (Point doubling) Let P = (x1,y1) ∈ E(Fp), where P ≠ -P. Then 2P = (x3,y3), where

   \[x3 = \left(\frac{3x1^2+a}{2y1}\right)^2 - x1 - x1 \quad \text{and} \quad y3 = \left(\frac{3x1^2+a}{2y1}\right)^2(x1 - x3) - y1\]

ECDSA Key Pair Generation

An entity A’s key pair is associated with a particular set of EC parameters D = (n, a, b, G, p, hash). This association can be assured cryptographically (e.g., with certificates) or by context (e.g., all entities use the same domain parameters). The entity A must have the assurance that the domain parameters are valid prior to key generation.

For ECDSA key pair generation, each entity A does the following:

1. Select a random or pseudorandom integer “Pri” in the interval [1, n − 1].

2. Compute Pub = Pri * G.

3. A’s public key is “Pub”; A’s private key is “Pri”.

ECDSA Signature Generation and Verification

Signature

To sign a message m, an entity A with domain parameters D = (n, a, b, G, p, hash) and associated key pair (Pri, Pub) does the following:

1. Select a random or pseudorandom integer k, 1 ≤ k ≤ n − 1.

2. Compute k * G = (x1,y1) and convert x1 to an integer x̄1.

3. Compute R = x1 mod n. If r = 0 then go to step 1.

4. Compute k⁻¹ mod n.

5. Compute SHA − 1(m) and convert this bit string to an integer “hash”.

6. Compute S = k⁻¹(hash + Pri * R) mod n. If S = 0 then go to step 1.

7. A’s signature for the message m is (R,S).

Verification

To verify A’s signature (R,S) on m, B obtains an authentic copy of A’s domain parameters D = (n,a,b,G,p,hash) and associated public key Q. B then does the following:

1. Verify the R and S are integers in the interval [1, n − 1].

2. Compute SHA − 1(m) and convert this bit string to an integer “hash”.

3. Compute S⁻¹ mod n.

4. Compute U₁ = hash * S⁻¹ mod n and U₂ = R * S⁻¹ mod n.

5. Compute X = U₁ * G + U₂ * Pub.

6. If X = O, then reject the signature. Otherwise, convert the x-coordinate x₁ of X to an integer x̄1, and compute v = x̄1 mod n.

7. Accept the signature if and only if v = R.

Proof that Signature Verification Works

If a signature (R,S) on a message m was indeed generated by A, then

S = k⁻¹(hash + Pri * R) mod n. Rearranging gives

\[k ≡ S⁻¹(hash + Pri * R) ≡ S⁻¹ * hash + S⁻¹ * Pri * R ≡ U₁ + U₂ * Pri (mod n)\]

Thus

\[U₁ * G + U₂ * Pub = (U₁ + U₂ * Pri) * G = k * G\]

and so v = R as required.

Features

Supported operations:

• Verification (reg_mode_sel == 2’d0)

• Signature (reg_mode_sel == 2’d1)

• Scalar multiplication (reg_mode_sel == 2’d2, {eng_xo, eng_yo} = eng_h * {eng_x, eng_y})

• Basic function (reg_mode_sel == 2’d3)

reg_func_sel[2:0]	Function description
1XX	add_point: {eng_xo, eng_yo} = {eng_x, eng_y} + {eng_gx, eng_gy}
000	sub_mod: {eng_xo, eng_yo} = (eng_x - eng_y) % prime
001	div_mod: {eng_xo, eng_yo} = (eng_x/eng_y) % prime
010	add_mod: {eng_xo, eng_yo} = (eng_x + eng_y) % prime
011	mul_mod: {eng_xo, eng_yo} = (eng_x * eng_y) % prime

Block Diagram

Functional Description

The ECDSA implements a complete asymmetric (public/private) key cryptographic signature solution based upon Elliptic Curve Cryptography and the ECDSA signature protocol. The device features hardware acceleration for the NIST standard Secp256k1 and P256 prime curve includes ECDSA signature generation, ECDH key agreement, and ECDSA public key signature verification.

Startup Step

1. Enable the clock, and set reg_eng_clk enable = 1. (0x000)

2. Reset the ECDSA, reg_eng_rst = 1. (0x000)

3. Reset the ECDSA, reg_eng_rst = 0. (0x000)

4. Set the input data.

5. Set eng_start = 1. (0x008)

ECDSA Interrupt

The assertion of the ECDSA interrupt occurs when the calculation is completed. When the interrupt is occurred the software can access the EISR (0x008) to identify the interrupt type.

Registers

Introduction

The ECDSA has a number of internal registers that are accessed through the 12-bit address bus.

reg_mode_sel=0, verification

Input	Pin Name	Offset
public key x	eng_x	0x010~0x02C
public key y	eng_y	0x030~0x04C
hash	eng_h	0x150~0x16C
R	eng_verify_r	0x110~0x12C
S	eng_verify_s	0x130~0x14C
base point x (gx)	eng_gx	0x050~0x06C
base point y (gy)	eng_gy	0x070~0x08C
cor_a	cor_a	0x170~0x18C
prime	prime	0x190~0x1AC
order_n	order_n	0x1B0~0x1CC

Output	Pin Name	Offset
R_x	eng_xo	0x090~0x0AC
R_y	eng_yo	0x0B0~0x0CC
verify_pass	verify_pass	0x008
verify_err	verify_err	0x008
infinity_err	infinity_err	0x008
eng_finish	eng_finish	0x008

reg_mode_sel=1, signature

Input	Pin Name	Offset
private key	eng_x	0x010~0x02C
random k	eng_y	0x030~0x04C
hash	eng_h	0x150~0x16C
base point x(gx)	eng_gx	0x050~0x06C
base point y(gy)	eng_gy	0x070~0x08C
cor_a	cor_a	0x170~0x18C
prime	prime	0x190~0x1AC
order_n	order_n	0x1B0~0x1CC

Output	Pin Name	Offset
public key x	eng_xo	0x090~0x0AC
public key y	eng_yo	0x0B0~0x0CC
R	eng_sign_r	0x0D0~0x0EC
S	eng_sign_s	0x0F0~0x10C
sign_err	sign_err	0x008
infinity_err	infinity_err	0x008
eng_finish	eng_finish	0x008

reg_mode_sel=2, scalar multiplication

Input	Pin Name	Offset
private key	eng_h	0x150~0x16C
base point x (gx)	eng_x	0x010~0x02C
base point y (gy)	eng_y	0x030~0x04C
cor_a	cor_a	0x170~0x18C
prime	prime	0x190~0x1AC
order_n	order_n	0x1B0~0x1CC

Output	Pin Name	Offset
public key x	eng_xo	0x090~0x0AC
public key y	eng_yo	0x0B0~0x0CC
share_key_err	share_key_err	0x008
infinity_err	infinity_err	0x008
eng_finish	eng_finish	0x008

reg_mode_sel=3, basic function

Input	Pin Name	Offset
eng_x	eng_x	0x010~0x02C
eng_y	eng_y	0x030~0x04C
eng_gx	eng_gx	0x050~0x06C
eng_gy	eng_gy	0x070~0x08C
cor_a	cor_a	0x170~0x18C
prime	prime	0x190~0x1AC

Output	Pin Name	Offset
public key x	eng_xo	0x090~0x0AC
public key y	eng_yo	0x0B0~0x0CC
infinity_err	infinity_err	0x008
eng_finish	eng_finish	0x008

Field Description

RTL8721DxRTL8720ERTL8726ERTL8713ERTL8730E

NA.

Flow Chart

I/O Ports

Clock and Reset

Port name	Width	Direction	Description
apb_clk	1-bit	I	APB interface clock
rst_n	1-bit	I	APB interface reset
eng_clk	1-bit	I	engine clock

APB Interface

Port name	Width	Direction	Description
apb_paddr	32-bit	I	APB address bus.
apb_pwrite_i	1-bit	I	APB write control
apb_psle_i	1-bit	I	APB peripheral select
apb_penable_i	1-bit	I	APB enable control
apb_pwdata_i	32-bit	I	APB write data bus
apb_pstrb_i	4-bit	I	APB write strobe
apb_pprot_i	3-bit	I	APB protection signal
apb_prdata_o	32-bit	O	APB read data bus
apb_pready_o	1-bit	O	APB slave ready.
apb_pslverr_o	1-bit	O	APB transfer failure.

Others

Port name	Width	Direction	Description
ecdsa_dbg_o	32-bit	O	Debug signals.
scan_mode	1-bit	I	Scan mode control signal.
scan_en	1-bit	I	Scan mode enable signal.
ecdsa_int	1-bit	O	Interrupt